Page updated:
April 6, 2021
Author: Collin Roesler
View PDF
Absorption Overview
Collin Roesler and Curtis Mobley contributed to this page.
When light interacts with matter one of three things can occur:
- Absorption:
- The light can disappear, with its radiant energy being converted into other forms, such as the energy of a chemical bond or heat.
- Elastic Scattering:
- The light can change direction, without a change of wavelength.
- Inelastic Scattering:
- The light can undergo a change of wavelength, usually to a longer wavelength, and usually in a different direction.
This page begins the discussion of the first of these processes. Scattering is described in the Scattering Chapter beginning at Scattering Overview.
Why is Absorption Important?
If you are interested in phytoplankton physiology, absorbed light is what matters. Light absorbed by phytoplankton provides the energy that drives photosynthesis; light elastically scattered by phytoplankton has no effect on photosynthesis and is of less interest to a plankton biologist. Therefore many more papers have been published on absorption by phytoplankton than on scattering by phytoplankton. Similarly, it is only the light that is absorbed by water molecules that heats water.
Phytoplankton absorption spectra are determined by the pigments in phytoplankton, hence measurement of phytoplankton absorption spectra gives information about what pigments are present and in what amounts. Thus absorption is fundamental to under standing phytoplankton physiology. Similarly, measurement of total absorption can be used to extract the amounts of phytoplankton, colored dissolved organic matter (CDOM), non-algal particles, or pollutants (if present) in the water column.
Some optical quantities are determined almost entirely by absorption. For example, the diffuse attenuation coefficient for downwelling plane irradiance, , is a very “absorption-like” apparent optical property. The depth dependence of the downwelling plane irradiance, , can be written as
where is the average of over depths 0 to . To first order,
Here is the backscatter coefficient and is the average cosine of the downwelling radiance distribution. In most waters, ; and the average cosine can be approximated by the cosine of the Sun’s direct beam angle, , as transmitted through a level sea surface. Thus a measured profile of the absorption coefficient allows for an approximate computation of , which in turn is directly related to the heating rate of the upper ocean (see Gershun’s Law).
Although ocean-color remote sensing measures scattered light leaving the oceans, the goal of that remote sensing is often to deduce how absorption in the water column changed sunlight into the scattered light that was measured. Knowing the effect of absorption gives a wealth of information about the state of the water column.
However, both absorption and scattering are equally important to the prediction and understanding of light propagation.
Both absorption and scattering affect visibility in ways that are illustrated in Fig. 1. Absorption removes light from a beam and thus makes a distant image darker. Wavelength-dependent absorption also alters the color of a distant image, as seen in the right panel of the figure.

Absorption by Oceanic Components
Unlike scattering, which is weakly spectrally dependent, absorption is highly spectrally dependent. The magnitude and spectral features depend upon the concentration and composition of the particulate and dissolved constituents and water itself. The inherent optical properties (IOPs) are conservative properties and therefore the magnitude of the absorption coefficient varies linearly with the concentration of the absorbing material. Theoretically, the absorption coefficient can be expressed as the sum of the absorption coefficients of each component:
| (1) |
Where is the total number of components and indicates the component, and all absorption is spectral, indicated by .
Practically, however, it is not possible to measure the absorption properties of each individual absorbing component and thus the individual components can be grouped into similarly absorbing constituents based upon similarity in their optical properties and/or analytically-based groupings:
| (2) |
where subscripts w, phyt, NAP and CDOM indicate water, phytoplankton, non-algal particles, and colored dissolved organic matter, respectively.
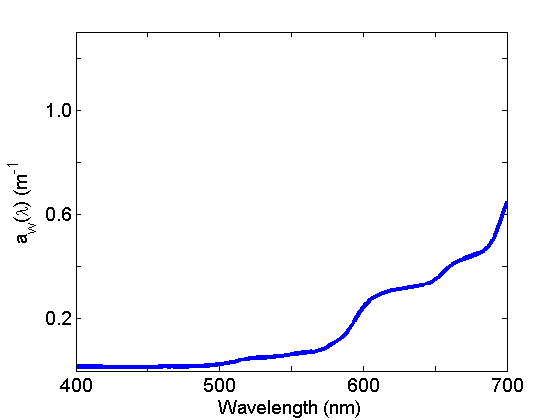
Absorption by water (Fig. 2) is weak in the blue and strong in the red and varies with temperature and salinity. See the page on Water for further discussion.
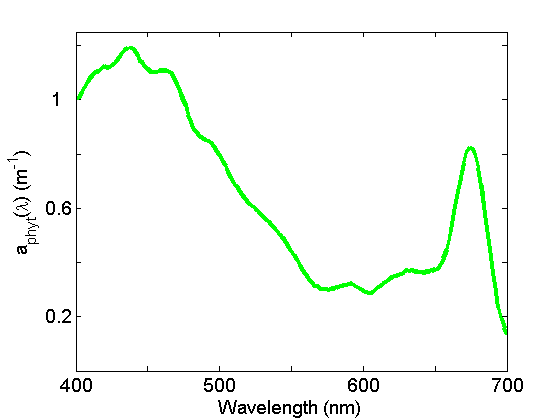
Absorption by particles is separated into phytoplankton and non-algal particles (NAP) using spectrophotometry and an extractive technique. Phytoplankton absorption (Fig. 3) demonstrates the most spectral variations of any of the components due to the individual pigment absorption spectra but in general exhibits peaks in the blue and red regions of the spectrum due to the ubiquitous presence of chlorophyll a. See the page on See the page on Phytoplankton for further discussion.
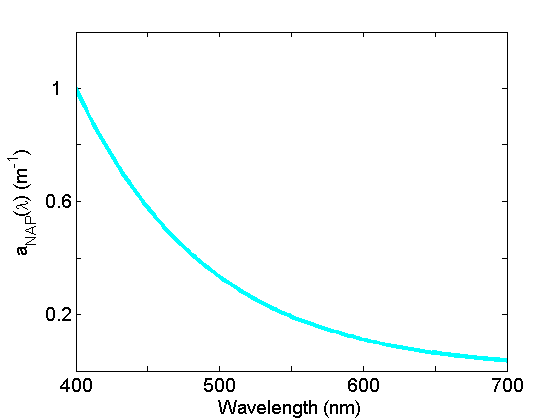
Non-algal particle absorption (Fig. 4) is strongest in the blue, decreasing approximately exponentially to the red. This component, operationally-defined, includes living zooplankton and bacteria, as well as the non-pigmented parts of phytoplankton (cell walls, membranes etc), detrital material as well as inorganic particles. See the page on Non-algal Particles for further discussion.
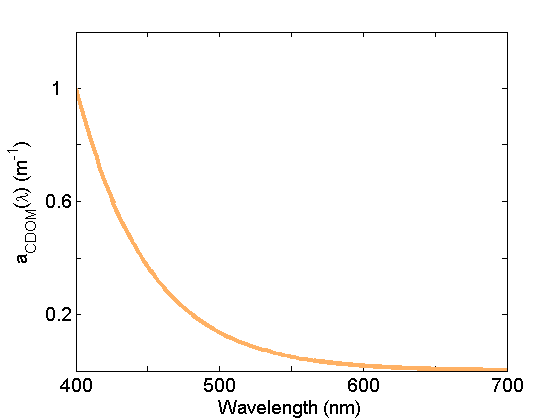
Colored dissolved organic matter (CDOM) absorption (Fig. 5) is very similar to that of NAP due in part to the similarity in composition (organic material), but generally exhibits a steeper exponential slope. This material is operationally separated from NAP by filtration; CDOM is measured on the filtrate passing through 0.2mm or 0.7 mm nominal pore sized filters. See the page on CDOM for further discussion.
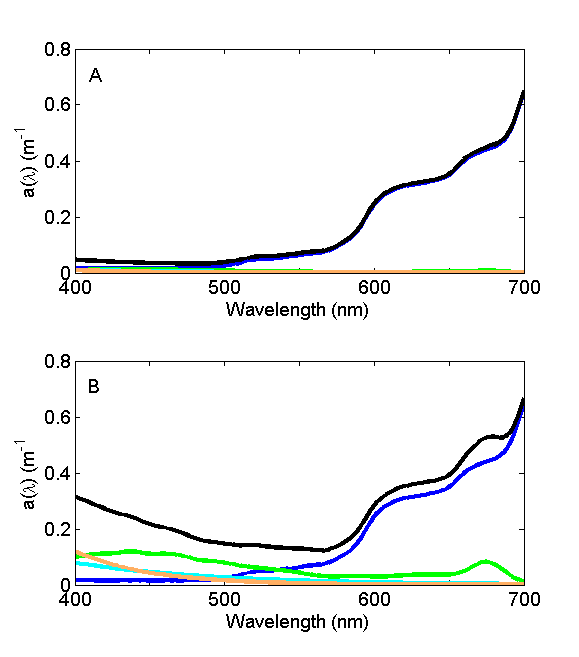
For oligotrophic environments with very low concentrations of suspended and dissolved material, the absorption coefficient is dominated by water (Fig. 6A) and the wavelength of minimum absorption is in the blue, hence the blue color of the seawater. For eutrophic and/or coastal environments with high concentrations of suspended and dissolved material (Fig. 6B), the absorption coefficient is dominated by that material and the wavelength of minimal absorption shifts to the green, lending green color to that environment.

 See comments posted for this page and leave your own.
See comments posted for this page and leave your own.