Page updated:
May 19, 2021
Author: Curtis Mobley
View PDF
Inherent Optical Properties
When light interacts with matter one of two things can happen. The light can disappear, with its energy being converted to another form such as heat or the energy contained in a chemical bond. This process is called absorption. The light can also change its direction and/or wavelength. Either of these processes is called scattering.
The absorption and scattering properties of a medium such as sea water are described by its inherent optical properties, or IOPs. IOPs are properties of the medium and do not depend on the ambient light field. That is, a volume of water has well defined absorption and scattering properties whether or not there is any light there to be absorbed or scattered. This means that IOPs can be measured in the laboratory on a water sample, as well as in situ in the ocean.
Conceptual Definitions of IOPs
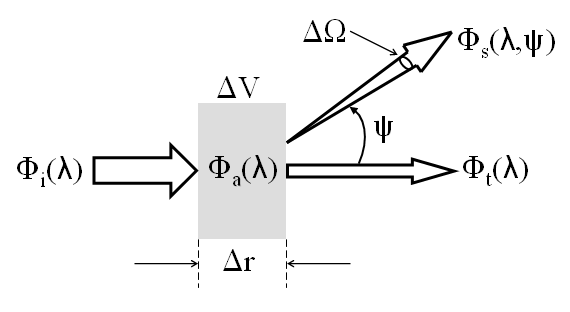
The absorption coefficient is the fundamental IOP that describes how a medium absorbs light. The volume scattering function likewise describes how the medium scatters light. If you know these two IOPs, then you know everything there is to know about the medium interacts with unpolarized light. Other IOPs are sometimes convenient, and they can be defined in terms of the absorption coefficient and the volume scattering function. Figure 1 is the key to defining the IOPs.
Consider a small volume of water, of thickness , illuminated by a collimated beam of monochromatic light of spectral radiant power at some wavelength , in , as illustrated in Fig. 1. Some part of the incident power is absorbed within the volume of water. Some part is scattered out of the beam at an angle , and the remaining power is transmitted through the volume with no change in direction. Let be the total power that is scattered into all directions. Furthermore, assume that the light does not undergo a change in wavelength during the scattering process. Then by conservation of energy,
The absorptance is the fraction of incident power that is absorbed within the volume:
Likewise, the scatterance is the fractional part of the incident power that is scattered out of the beam into all directions,
and the transmittance , the fraction of the incident power that passes through the volume without interacting with the medium, is
Clearly, = 1.
The inherent optical properties usually employed in optical oceanography are the absorption and scattering coefficients, which are respectively the absorptance and scatterance per unit distance in the medium. In the geometry of Fig. 1, let the thickness approach zero, in which case only a decreasingly small fraction of the incident power is absorbed. The absorption coefficient is then defined as
| (1) |
Likewise the scattering coefficient is defined as
| (2) |
where is the fraction of scattered power.
The beam attenuation coefficient is defined as
| (3) |
Another commonly used IOP is the single-scattering albedo , defined by
| (4) |
In waters and at wavelengths where the beam attenuation is due primarily to scattering, is near one. For waters and wavelengths where the beam attenuation is due primarily to absorption, is near zero. As we shall see elsewhere, the single-scattering albedo is the probability that a light ray (commonly called a photon) will be scattered (rather than absorbed) in any given interaction, hence is also known as the probability of photon survival in any given interaction between a ray or photon and matter.
The IOPs depend on the composition, morphology, and concentration of the particulate and dissolved substances in the ocean. Composition refers to what materials make up the particle or dissolved substance, in particular to the index of refraction of that material relative to that of the surrounding water. Morphology refers to the sizes and shapes of particles. Concentration refers the number of particles in a given volume of water, which is described by the particle size distribution, or to the amount of a dissolved substance in the water. As we will see, different materials absorb much differently as a function of wavelength. Particles with different shapes scatter light differently, even if the particles have the same volume. Particles with different volumes scatter light differently even if they have the same shape. Consider, for example, atmospheric visibility through rain or fog. Even if the total water content per cubic meter of air is the same, you can “see through” a few large raindrops, whereas many small fog droplets greatly reduce visibility.
Because the physical characteristics of the dissolved and particulate substances in the ocean vary by orders of magnitude, so do the IOPs. For example, both the absorption and scattering coefficients of pure water are less that 0.01 1/m at 440 nm. However, in turbid coastal waters with high concentrations of phytoplankton, mineral particles, and dissolved organic matter, the absorption and scattering coefficients can be four orders of magnitude larger. The volume scattering function (at a given scattering angle and wavelength) can also vary by orders of magnitude between open ocean and coastal waters. Understanding how variability in IOPs is determined by the various constituents of the ocean is a fundamental problem of optical oceanography.
Comment: Equations (1) and (2) are conceptual, mathematical definitions in terms of limits. These definitions are not suitable for implementation in measurement instruments, which always have a finite path length and finite and . The page on measuring IOPs shows how to recast the conceptual definitions into forms suitable for making measurements.
Historical IOP Notation
Just as with the radiometric quantities, there is an “historical” set of symbols in addition to the IAPSO recommended symbols used above. Table 1 summarizes the IOP’s as they are commonly employed in optical oceanography.
| Quantity | SI Units | Recommended Symbol | Historical Symbol |
| absorption coefficient | |||
| scattering coefficient | |||
| backward scattering coefficient | |||
| forward scattering coefficient | |||
| beam attenuation coefficient | |||
| volume scattering function | |||
| scattering phase function | |||
| single-scattering albedo | dimensionless | or |

 See comments posted for this page and leave your own.
See comments posted for this page and leave your own.