Petzold's Measurements

Several early researchers in optical oceanography built instruments to measure the volume scattering function (VSF) of oceanic waters. [See Jerlov (1976) for data and references for early measurements.] The most carefully made and widely cited scattering measurements are found in the classic report of Petzold (1972) (summarized in Petzold, 1977). He combined two instruments, one for VSF measurements at very small angles ($\psi =$ 0.172, 0.344, and 0.688 deg) and one for angles between 10 and 170 degrees, to obtain VSF measurements over almost the whole range of scattering angles. Petzold’s report describes his instruments, their calibration and validation, and tabulates data from very clear (Bahamas), productive coastal (California), and turbid harbor (San Diego, California) waters. The Petzold VSFs and phase functions plotted on this page can be downloaded.

Figure 1 shows three of Petzold’s VSF curves displayed on a log-log plot to emphasize the forward scattering angles. The same data are displayed on log-linear axes in Fig. 2, which emphasizes large scattering angles. The instruments he used had a spectral response centered at $\lambda =514nm$ with a bandwidth of 75 nm (full width at half maximum). In these figures the top (red) curve was obtained in the very turbid water of San Diego Harbor, California; the center (green) curve comes from near-shore coastal water in San Pedro Channel, California; and the bottom (blue) curve is from very clear water in the Tongue of the Ocean, Bahama Islands. The striking feature of these volume scattering functions from very different waters is the similarity of their shapes.

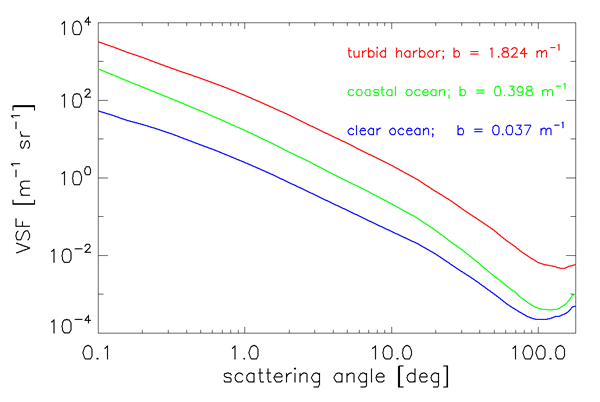
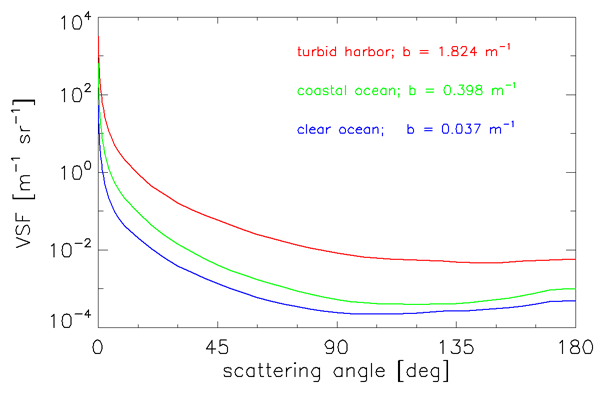
Although the scattering coefficients $b$ of the curves in Figs. 1 and 2 vary by a factor of 50, the uniform shapes suggest that it may be reasonable to define a “typical” particle phase function ${\tilde{\beta }}_{\text{p}}\left(\psi \right)$. This has been done with three sets of Petzold’s data from waters with a high particulate load (one set being the top curve of Figs. 1 and 2), as follows (Mobley et al., 1993):

1.

Subtract the pure sea water VSF at 514 nm from each curve to get three particle volume scattering functions ${\beta }_{\text{p}}^i\left(\psi \right),i=1,2,3$.

2.

Obtain the corresponding particle scattering coefficients from $b_{\text{p}}^i=b^i-b_{\text{water}}$;

3.

Compute three particle phase functions via ${\tilde{\beta }}_{\text{p}}^i\left(\psi \right)={\beta }_{\text{p}}^i\left(\psi \right)∕b_{\text{p}}^i$;

4.

Average the three particle phase functions at each scattering angle to define the “average particle” phase function.

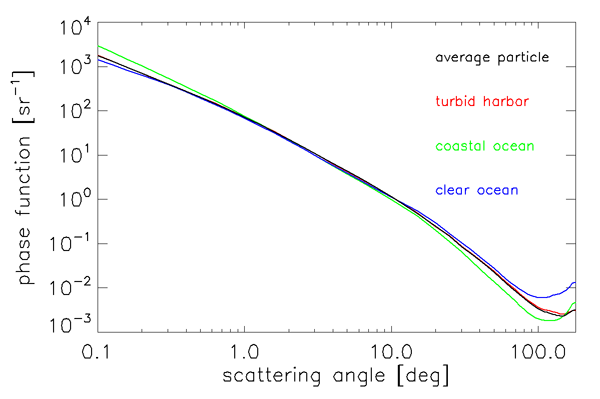
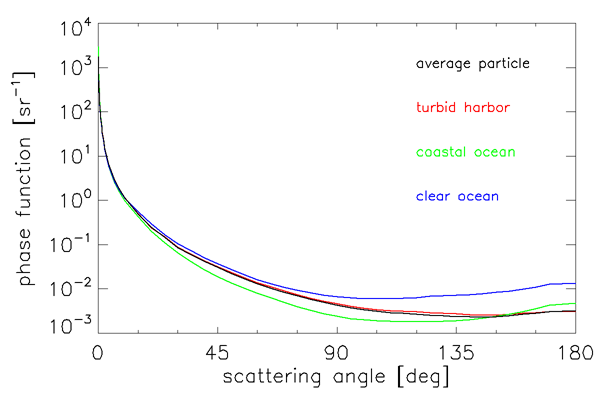
The three phase functions so obtained and the average-particle phase function are shown in Figs. 3 and 4. This average-particle phase function satisfies the normalization condition $2\pi {\int \; <!--nolimits-->}_0^{\pi }{\tilde{\beta }}_{\text{p}}\left(\psi \right)sin\psi d\psi =1$ if a behavior of ${\tilde{\beta }}_{\text{p}}\propto {\psi }^{-m}$ is assumed for $\psi <0.1deg$ and a trapezoidal-rule integration is used for $\psi \ge 0.1deg$, with linear interpolation in $log{\tilde{\beta }}_{\text{p}}\left(\psi \right)\text{versus}log\psi$ used between the tabulated values. Here $m=1.346$ is the negative of the slope of $log{\tilde{\beta }}_{\text{p}}\text{versus}log\psi$, as determined from the two smallest measured scattering angles.

This “Petzold average particle” phase function has been widely used in radiative transfer calculations and is one of the standard phase functions available in HydroLight. However, it must be remembered that this phase function is based on very limited data from turbid harbor waters at one wavelength and likely corresponds to a mixture of phytoplankton and mineral particles as might be found in harbor waters. This phase function thus corresponds closely to the turbid harbor phase function seen in Figs. 3 and 4.

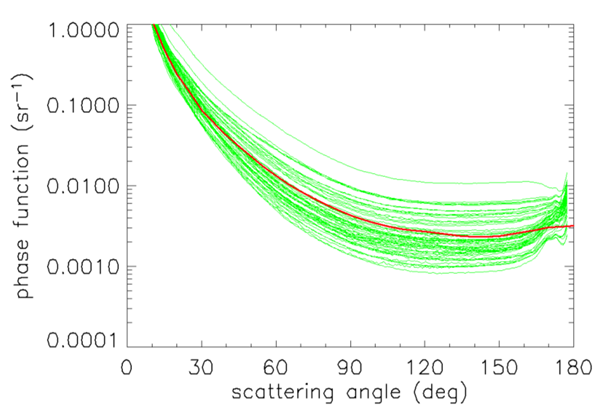
Figure 5 compares the Petzold average phase function with 62 phase functions measured in coastal waters at 530 nm using the more recently developed VSM (volume scattering meter) instrument of Lee and Lewis (2003). The Petzold average particle phase function does indeed give a good average for these phase functions. However, it is important to note that there is an order-of-magnitude variability in the VSM phase functions at backscattering angles. The large variability in the measured phase functions of Fig. 5 will give corresponding variability in the remote-sensing reflectance, for example.

Thus, as is always the case with a simple model, the average-particle phase function may be satisfactory on average, but may be very wrong in a simulation of a particular water body. When attempting to model a particular water body, it is always best to use a VSF or phase function measured at the particular time and place being modeled, rather than relying on a “generic” phase function or analytic model. Examples of this are given in Mobley et al. (2002).