Surface Reflectance Factors

This page links to the extensive data files of the surface reflectance factors $\rho \left({𝜃}_{sun},{𝜃}_v,{\varphi }_v,U\right)$ described in Mobley (1999) and Mobley (2015). The first paper discusses the problems inherent in estimating the remote-sensing reflectance $R_{rs}$ from measurements of the sky and ocean radiance made from just above the sea surface. That paper used Cox-Munk sea surfaces and unpolarized ray tracing to compute $\rho$ factors, which are given as the original table below. The second paper used sea surfaces generated from wave variance spectra and Fourier transforms, and polarized ray tracing, to re-evaluate the numerical values of the $\rho$ factors to account for the effects of polarization and sea surface elevation (wave shadowing). The recomputed $\rho$ values are given in the revised table. The comments below assume familiarity with these papers.

The original 1999 table gives $\rho$ values as a function of wind speed $U$ (0 to 14 m/s), sun zenith angle ${𝜃}_{sun}$ (0 to 80 deg), and viewing direction (10 deg in nadir angle ${𝜃}_v$ and 15 deg in azimuthal angle ${\varphi }_v$) for clear sky conditions at 550 nm. The revised 2015 table is similar. The $rho$ values of the revised table are based on better sea surface simulations and account for polarization effects, but only for a single-scattering Rayleigh sky. Such a sky is at best an approximation to an extremely clear sky.

Download the original rho table of the 1999 paper.

Download the revised rho table of the 2015 paper.

The key to converting the radiance measurements to $R_{rs}$ is having a good value for $\rho$, the proportionality factor that relates the radiance measured when the detector views the sky to the reflected sky radiance measured when the detector views the sea surface. That is, $\rho$ = (surface-reflected radiance)/(sky radiance) for the particular viewing geometry and environmental conditions. See Fig. 1 and Eq. (4) of the 1999 paper for the details.

It must be remembered that $\rho$ values vary—sometimes very little, but sometimes a lot—with wavelength. (HydroLight users can find the $\rho$ values in the last column of the printout labeled “Radiances Just Above the Water Surface.”) A few percent variation over visible wavelengths is expected from the wavelength dependence of the water real index of refraction. However, $\rho$ still varies even in a HydroLight run using a constant index of refraction (e.g., 1.34). The question thus arises, “How can $\rho$ vary with wavelength if the real index of refraction is constant, since $\rho$ describes how the sea surface reflects radiance, and the surface reflectance properties (i.e., the Fresnel reflectance) are determined by the index of refraction?” The answer lies in the observation that $\rho$ is not an inherent optical property of the sea surface.

The sky radiance distribution changes as a function of wavelength. In particular, the ratio of background sky to direct solar irradiance changes in the RADTRAN model that is used within HydroLight, even if the angular pattern stays the same. This means that there are different amounts of sun glitter being seen by the sensor at different wavelengths, all else (viewing geometry, wind speed, etc.) being the same. That in turn means that $\rho$ will have some wavelength dependence because the sky radiance changes even though the surface reflectance properties are the same at each wavelength.

This can be verified with a couple of HydroLight runs. Figure 1 shows $\rho$ as a function of wavelength for two viewing geometries. The wind speed was $6m{s}^{-1}$, the Sun was at 30 deg in a clear sky, and the water was Case 1 with a chlorophyll concentration of $1mg{m}^{-3}$. For this high sun angle and a nadir viewing direction (looking straight down), there is a significant amount of sun glitter within the instrument field of view. The amount of sun glitter depends on wavelength because the sky conditions depend on wavelength; $\rho$ thus varies by a factor of two between 350 and 800 nm. For the optimum viewing geometry, there is almost no sun glitter seen by the instrument, and $\rho$ is essentially independent of wavelength.

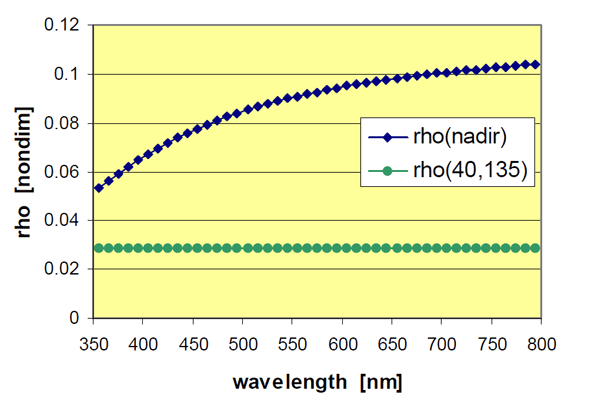
As commented in the last paragraph of section 5 of the 1999 paper, $\rho$ “... is strongly dependent on sky conditions, viewing geometry, sea state, and sometimes wavelength.” As seen above, if you hold the ocean and instrument conditions fixed but change the sky conditions, you change $\rho$. If you are viewing sun glitter, not only is the value of $\rho$ large, but it is also wavelength dependent. The table of $\rho$ values was generated for 550 nm. Its use at other wavelengths assumes that the sky conditions and viewing geometry are such that $\rho$ is nearly independent of wavelength.

The main purpose in writing the 1999 Applied Optics paper was to point out that $\rho$ is not an inherent optical property of the sea surface (as is the Fresnel reflectance), and that it’s really hard (actually impossible) to know what $\rho$ value to use in a particular situation. All you can do is make an educated guess and hope for the best. Fortunately, educated guesses often work pretty well if you’re careful to avoid sun glitter and cloud reflectance in partly cloudy skies.

Anyone using $\rho$ to remove surface glint to estimate the remote-sensing reflectance $R_{rs}$ should read the paper by Lee et al. (2010), which discusses wavelength dependence.

The 2015 paper was written to study the effects of more realistic sea surface simulations and polarization on sea surface optical properties. The last section of that paper re-evaluates $\rho$ and compares values computed with better sea surfaces and polarized ray tracing with the original values computed using Cox-Munk surfaces and unpolarized ray tracing. Sea surface reflectance properties depend on the polarization state of in incident radiance, and the polarization of the incident sky radiance varies greatly with direction relative to the sun, and with atmospheric properties. Not surprisingly, it was found that $\rho$ depends on the sky polarization. Although the qualitative dependence of $rho$ on sun zenith angle, viewing direction, and wind speed are similar for the polarized vs. unpolarized calculations, $\rho$ values computed with polarized ray tracing show greater variability with sun zenith angle and viewing direction for a given wind speed than do the values computed without accounting for sky polarization.