Cherenkov Radiation

Cherenkov radiation (Cherenkov (1934)) is electromagnetic radiation emitted by charged particles traveling faster than the phase speed of light in a dielectric medium such as water. It can be qualitatively thought of as the optical equivalent of the acoustic shock wave (“sonic boom”) generated by an airplane ﬂying faster than the speed of sound in air. Cherenkov radiation is the cause of the beautiful blue glow around the core of a water-cooled nuclear reactor as shown in Fig. 1. [The emission of light by a charged particle moving faster than the speed of light in a medium was ﬁrst predicted by Oliver Heavyside in a series of papers starting in 1888. Arnold Sommerfeld independently predicted the eﬀect in 1904, and Marie Curie observed the glow of light in radium solutions. However, these earlier results were unappreciated and forgotten until Cherenkov’s observations in the 1930s. You will see Cherenkov’s name romanized in various ways; the accent is on the last syllable.]

Figure 1: Photograph of Cherenkov radiation in a nuclear reactor core. [Public domain photograph from the U. S. Nuclear Regulatory Commission]

Bradner et al. (1987) examined physical sources of light in the ocean. They estimated that near the sea surface, Cherenkov radiation from cosmic rays generates a photon irradiance of order $1 0^{7} p h o t o n s s^{- 1} m^{- 2}$ ; this value decreases exponentially with depth with an e-folding distance of about 1 km. However, another source of Cherenkov radiation is due to the decay of radioactive potassium-40, which is distributed uniformly throughout the oceans as part of the dissolved salts that make up salinity.

The Earth’s crust contains potassium at a concentration of about 2.6% by mass. This potassium occurs as three isotopes: stable $^{39} K$ (93.2581%) and $^{41} K$ (6.7302%), and radioactive $^{40} K$ (0.0117%). $^{40} K$ decays 89.1% of the time to $^{40} C a$ by emission of an electron and an electron anti-neutrino (beta decay), and 10.9% of the time to $^{40} A r$ by capture of an inner-shell electron, followed by emission of a gamma ray and a neutrino. The half-life of $^{40} K$ is 1.25 Gy. [Earth’s atmosphere is 0.94% argon, of which 99.6% is $^{40} A r$ . Spectroscopy shows that the argon in stars is 85% $^{36} A r$ , which is created by fusion of two alpha particles (Helium nuclei) with one silicon-32 nucleus during supernova explosions, and 15% is $^{38} A r$ . It is thus thought that the argon in Earth’s atmosphere has accumulated up over billions of years from the decay of $^{40} K$ .]

When $^{40} K$ decays to $^{40} C a$ , the emitted electron and anti-neutrino carry a combined kinetic energy of 1.31 MeV or $2.1 \times 1 0^{- 13} J$ . There is a continuous distribution of the electron kinetic energy ranging from 0 to a maximum of 1.31 MeV, with the peak at about 0.55 MeV (Kelly et al. (1959)). [It is a characteristic of beta decay that the emitted electrons have a continuous spectrum of energies from 0 to some maximum. This contrasts with alpha decay, in which the emitted alpha particles have a single energy determined by the quantized energy levels of the decaying nucleus.] The associated speed of the electron for a given kinetic energy can be obtained from the formula for relativistic kinetic energy (e.g., Section 42-14 of Halliday and Resnick (1988)):

K E = m_{o} c^{2} (\frac{1}{\sqrt{1 - {(v ∕ c)}^{2}}} - 1),

where $m_{o}$ is the rest mass of the particle, $c$ is the speed of light, and $v$ is the speed of the particle. In relativity theory, it is customary to let $β = v ∕ c$ be the speed of a particle relative to the speed of light in a vacuum. Solving this equation for $β^{2} = {(v ∕ c)}^{2}$ gives

β^{2} = 1 - {(\frac{K E}{m_{o} c^{2}} + 1)}^{- 2} .

(1)

Using the values in Table 1 gives $β^{2} = 0.918$ , or $v = 0.958 c$ , for a 1.31 MeV electron. The phase speed of light in water is $c ∕ n$ , which is approximately $0.75 c$ at visible wavelengths. Thus the emitted electron is traveling faster than the speed of light in water and will therefore emit Cherenkov radiation until the electron slows down to less than $c ∕ n$ through loss of radiated energy and other interactions with the water.


Symbol	Quantity	Value

$m_{o}$	rest mass of the electron	$9.109 \times 1 0^{- 31} k g$
$e$	charge of the electron	$1.602 \times 1 0^{- 19} C$
$c$	speed of light in vacuo	$2.998 \times 1 0^{8} m s^{- 1}$
$h$	Planck constant	$6.626 \times 1 0^{- 34} J s$
$μ_{o}$	magnetic permeability of free space	$4 π \times 1 0^{- 7} N s^{2} C^{- 2}$
$K E$	kinetic energy of emitted electron	$1.31 M e V = 2.099 \times 1 0^{- 13} J$
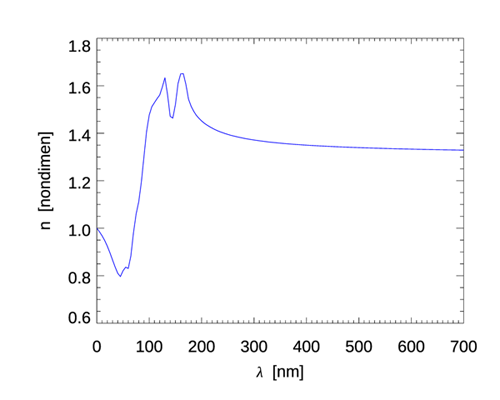
$n$	real index of refraction of water	see Fig. 2

Table 1: Quantities needed for Cherenkov radiation calculations of

^{40} K

decay.

The energy radiated by a single $^{40} K$ electron per unit of distance traveled ( $x$ , in meters) and per unit angular frequency ( $ω$ , in radians per second) of the emitted light is given by the celebrated formula of Frank and Tamm (1937):

\frac{\partial^{2} E}{\partial x \partial ω} = \frac{1}{4 π} e^{2} μ_{w} (ω) ω (1 - \frac{1}{β^{2} n^{2} (ω)}) [\frac{J}{m s^{- 1}}] .

(2)

Here $μ_{w} (ω)$ is the frequency-dependent magnetic permeability of the medium. [Although the end result is simple, the derivation of Eq. (2) starting from Maxwell’s equations is quite diﬃcult (e.g., Sections 13.4 and 14.9 of Jackson (1962)). Pavel Cherenkov, Ilya Frank, and Igor Tamm shared the 1958 Nobel Prize in Physics “for the discovery and the interpretation of the Cherenkov eﬀect.”]

Using $ω = 2 π c ∕ λ$ to convert the Frank and Tamm formula to energy emitted per unit distance per unit wavelength gives

\frac{\partial^{2} E}{\partial x \partial λ} = π c^{2} e^{2} μ_{w} (λ) \frac{1}{λ^{3}} (1 - \frac{1}{β^{2} n^{2} (λ)}) [\frac{J}{m m}] .

(3)

Converting this formula from energy emitted to number $N$ of photons emitted via $E = N h c ∕ λ$ gives

\frac{\partial^{2} N}{\partial x \partial λ} = \frac{π c}{h} e^{2} μ_{w} (λ) \frac{1}{λ^{2}} (1 - \frac{1}{β^{2} n^{2} (λ)}) [\frac{p h o t o n s}{m m}] .

(4)

The magnetic permeability $μ_{w}$ is a function of frequency (or wavelength), but for water its value equals that of a vacuum, $μ_{o}$ , the permeability of free space, to within a 8 parts per million. Therefore we can replace $μ_{w}$ with $μ_{o}$ in these equations with a negligible error. The observant reader will then note that

α = \frac{c e^{2} μ_{o}}{2 π h} = 0.007297 \approx \frac{1}{137}

is the dimensionless ﬁne-structure constant of quantum theory. The last equation therefore can be succinctly written as

\frac{\partial^{2} N}{\partial x \partial λ} = 2 π α \frac{1}{λ^{2}} (1 - \frac{1}{β^{2} n^{2} (λ)}) .

(5)

In these formulas, $x$ and $λ$ are in meters.

These formulas show a remarkable feature of Cherenkov radiation, namely that the emission is broad-band and increases rapidly going from visible to ultraviolet wavelengths. As seen in Fig. 2, the real index of refraction of water decreases rapidly between 130 nm, where $n \approx 1.63$ , and 71 nm, where $n$ drops to less than 1. [The discussion in Section TBD explains that that although $n < 1$ gives the phase speed $c ∕ n$ greater than the speed of light in vacuo, this is not a violation of special relativity.] This gives a sharp radiation cut-oﬀ at wavelengths less than about 100 nm because as $n$ approaches 1, the speed of light in water approaches the speed in vacuo, in which case the electron is always traveling slower than light in the water, and there is no emitted radiation. For infrared and longer wavelengths, the emission is small and goes to zero as the wavelength increases. The red curves in Fig. 3 show Eqs. (3) and (5) using the wavelength-dependent $n (λ)$ seen in Fig. 2 for the initial electron energy of 1.31 MeV. For wavelengths in the visible range, Table 2 of the water IOPs page shows that $n \approx 1.36$ even for the extreme case of cold (0 deg C), saline (35 PSU), deep-ocean (depth of 10,000 m) water, compared to about 1.34 for pure water at atmospheric pressure. This diﬀerence would have only a small eﬀect on the spectra plotted in Fig. 3, so these curves for pure water are representative of all parts of the ocean.

Figure 2: The real index of refraction of pure water for wavelengths between 0 and 700 nm. (redrawn from Fig. 1 of the water IOPs page.)

Figure 3: Cherenkov radiation spectra for a single

^{40} K

electron in optically pure water. The left panel shows the emitted energy per centimeter of travel and per nanometer of wavelength. The right panel shows the corresponding spectra for the number of emitted photons. The red curves are for the initial electron with an energy of 1.31 MeV. The blue curves are for an energy of 0.27 MeV, below which there is no more emission at wavelengths longer than 300 nm. The green curves are for an energy of 0.17 MeV,

v^{2} ∕ c^{2} = 0.434

, for which there is only a small amount of emission at the UV wavelengths where the index of refraction greater than 1.52.

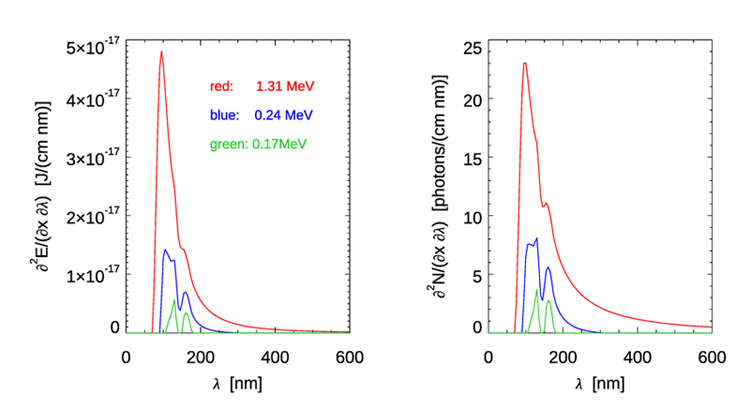
Numerically integrating Eq. (3) over wavelength, for a given value of $β$ , gives the energy emitted over all wavelengths per unit distance traveled. Further integrating over distance gives the total energy emitted. Corresponding integrations of Eq. (5) give the numbers of emitted photons. As the electron travels through the water, its kinetic energy decreases. When the kinetic energy decreases to a value such that the electron’s speed, given by Eq. (1), results in $v = c ∕ n (λ)$ , photon emission ceases for that wavelength. After the kinetic energy has decreased to 0.24 MeV, $β^{2} = 0.533$ . This gives $v < c ∕ n (λ)$ for $n (λ) \leq 1.37$ . There is thus no more radiation for wavelengths greater than 300 nm, where $n \leq 1.37$ . The spectra at this energy are shown in blue in Fig. 3. The green curves in the ﬁgure are for an energy of 0.17 MeV, $β^{2} = 0.434$ , for which there is only a small amount of emission at the UV wavelengths where the index of refraction greater than 1.52. To compute the total amount of Cherenkov radiation, the above integrations over wavelength and distance must be repeated for each energy of the distribution of energies of the emitted electrons; thus there is a triple integration over energy, wavelength, and distance.

Equations (2)-(5) are correct in that they give the energy or number of photons emitted as Cherenkov radiation for a given electron energy. What they do not tell you is that less than one percent of the kinetic energy of of an electron emitted by a $^{40} K$ nucleus results in Cherenkov radiation. Almost all of the electron’s energy goes into ionizing water molecules as the electron travels through the water. This loss of energy to ionization is given by an equation known as the Bethe-Bloch formula. [For a derivation and discussion see Chapter VII, Section 5 of Arya (1966). The Bethe-Bloch formula involves two additional parameters: the energy required to ionize a water molecule and the density of electrons in water (the number of water-molecule electrons per cubic meter). My evaluation of the Bethe-Bloch formula shows that for a 1.31 MeV electron, the energy lost to ionization is 153 times that lost to Cherenkov radiation.] Discussion of that calculation takes us beyond the needs of optical oceanography and will not be given here because the end result has been calculated by the physicists who use Cherenkov radiation for the detection of neutrinos in the deep ocean.

When a neutrino interacts with matter (which is extremely rare), the result can be a charged particle such as an electron or muon traveling in almost the same direction as the neutrino. Those charged particles also cause Cherenkov radiation, which can be detected as a function of time and direction and used to determine the direction and energy of the initial neutrino. Several neutrino detectors based on this idea have been built at the bottom of the ocean and deep within the ice at the geographic South Pole [To learn more, the keywords to search for are DUMAND (Deep Underwater Muon and Neutrino Detector; 1976-1995) and ANTARES (Astronomy with a Neutrino Telescope and Abyss environmental RESearch project; operational since 2008) in the ocean. AMANDA (Antarctic Muon And Neutrino Detector Array) and IceCube Neutrino Observatory are at the South Pole]. These detectors are arrays of thousands of photomultiplier tubes (PMTs), occupying as much as a cubic kilometer of space, that track the movement of the Cherenkov “light cone” as the particle travels through the detector. In deep-ocean measurements, Cherenkov radiation from $^{40} K$ decay is background noise imposed on the signal of interest. The magnitude of this Cherenkov background therefore has been carefully calculated and measured as part of the deep-ocean neutrino detector designs.

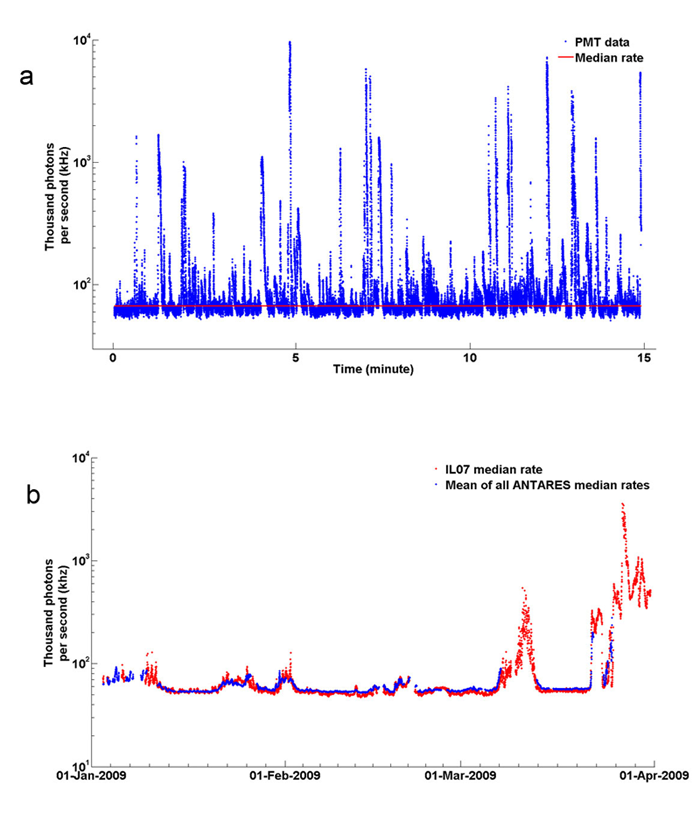
Use of the above formulas to compute the number of Cherenkov photons per square meter per second in the ocean must account for number of decaying $^{40} K$ atoms per cubic meter (about $12000 m^{- 3} s^{- 1}$ , of which 89.1% result in electron emission) and the clarity of the water (usually close to that of pure water in the deep ocean). Calculations predict about $1.2 \times 1 0^{6} p h o t o n s m^{- 2} s^{- 1}$ at visible wavelengths (400-700 nm) in clear ocean water (Learned et al. (1981), Bradner et al. (1987)). Nighttime measurements to depths of 4300 m in clear waters near Hawaii showed a typical background “glow” of order $1 0^{7} p h o t o n s m^{- 2} s^{- 1}$ , which includes bioluminescence as well as Cherenkov radiation. Aoki et al. (1986) report $2.1 8_{- 28 %}^{+ 9 %} \times 1 0^{6} p h o t o n s m^{- 2} s^{- 1}$ at the same location. Tamburini et al. (2013) recorded a 2.5 year times series of light at 2,500 m depth in the Mediterranean Sea. Each of their photomultiplier tubes (PMTs) recorded a steady background of $37, 000 \pm 3000 p h o t o n s s^{- 1}$ attributable to $^{40} K$ decay, plus another $40, 000 \pm 3000 p h o t o n s s^{- 1}$ attributable to background bioluminescence. During periods of strong currents, which triggered bioluminescence in the wakes of the PMTs, the bioluminescence signal increased by as much as a factor of 100; Fig. 4 shows some of their data. Their PMTs had a collection area of $0.038 m^{2}$ , so $37, 000 p h o t o n s s^{- 1}$ received by a PMT corresponds to about $1 0^{6} p h o t o n s m^{- 2} s^{- 1}$ , consistent with the predictions in the other papers. The measured total of $67, 000 p h o t o n s s^{- 1}$ for Cherenkov and background bioluminescence corresponds to $1.8 \times 1 0^{6} p h o t o n s m^{- 2} s^{- 1}$ . Thus it is never completely dark at even the greatest depths, even though no solar photons are present. [The PMTs were Hamamatsu model R7081-20. The data sheet gives a “minimum eﬀective area” of 220 mm. Taking this as the diameter of the PMT collector gives a collector area of $0.038 m^{2}$ . The PMT was sensitive to wavelengths from 300 to 650 nm with peak sensitivity at 420 nm.]

Figure 4: Measured bioluminescence and Cherenkov radiation photon counts in the Mediterranean Sea at 2500 m depth. Top panel: the photon counts in thousands per second for one PMT over a time of 15 minutes. Bottom panel: median photon counts from one particular PMT (red) and the average of the median rates for the 885 detectors in the array (blue) over a period of 3 months. Reproduced from Fig. S2 of Tamburini et al. (2013) under a Creative Commons Attribution License.

Most vertebrates, humans in particular, see only black-and-white in dim light using the rod cells in their retinas. (Cone cells are used for color vision in bright light; see the page on Color Vision.) The optically sensitive part of these rod cells is a single kind of photopigment known as an opsin (generally rhodopsin-1). A recent genetic study of 101 species of deep-sea ﬁsh Musilova et al. (2019) found that some ﬁsh express genes for coding multiple types of opsins, as many as 2 cone and 38 rod opsins in one species. The peaks of the wavelength sensitivities of these multiple opsins cover a range of blue to near-UV wavelengths. Thus it is hypothesized that some ﬁsh may be able to “see color” even in the dimmest light of the deep ocean. Giant squid have the largest eyes of any animal, around 30 cm in diameter. It is thought that they may be able to detect bioluminescence generated by their arch-enemies the sperm whales and know it’s time to leave. It may be that squid and other deep-ocean animals just see blobs of light or shadows against the faint background. If they see a small blob of light/shadow, eat it; if it’s a big blob/shadow, ﬂee. In addition, Frank and Widder (1996) found that the eyes of certain deep-sea crustaceans are equally sensitive to near-UV and blue-to-green visible wavelengths. Their paper discussed the penetration of near-UV solar radiation to depth. However, it can be speculated that these animals may have evolved eyes capable of seeing the low level of Cherenkov UV light. Assuming an average wavelength of 420 nm, the deep-ocean measurements of $1.8 \times 1 0^{6} p h o t o n s m^{- 2} s^{- 1}$ (Tamburini et al. (2013)) and $2.2 \times 1 0^{6} p h o t o n s m^{- 2} s^{- 1}$ (Aoki et al. (1986)) correspond to an irradiance of approximately $1 0^{- 12} W m^{- 2}$ , which is the threshold sensitivity of the eyes of some deep-sea ﬁsh as estimated from comparative anatomy studies by Denton and Warren (1957). This is probably not a coincidence.

Cherenkov Radiation

Comments for Cherenkov Radiation: